How To Find Tension Force With Angles

We can encounter in the illustration below that the force, F, needed to elevator the object is equal to the weight, West, of the object. This idea is the key concept that underlies our tension force formula. Likewise shown below is the free-body diagram of the object which shows the tension forces, T, acting in the string. As you lot tin can see, the tension forces come in pairs and in reverse directions:

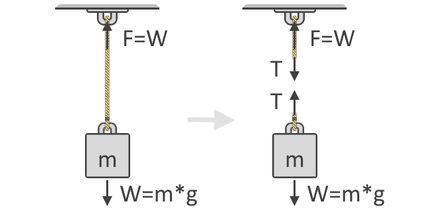
Illustration of an object being lifted using a string and its corresponding free-body diagram that shows forces acting in the system

Following Newton's Second Law of Motion, we can then express the summation of forces using the gratis-body diagram of the object, as shown on the right side of the analogy above. We use free-body diagrams to show the different directions and magnitudes of the forces that act on a body. In equilibrium, these forces should all equate to naught. Because all upward forces as positive and downward as negative, our equation is:

ΣF↑ = 0 = T + (-W)

T = West

where weight, West, becomes negative since it is directed downward. By transposing West to the other side of the equation, we can at present see that the tension strength in the rope is equal to the weight of the object it carries, as also shown to a higher place.

If we use more than ropes to elevator the object, the total tension force gets divided upward into the ropes. The tension force in each rope depends on their angles with respect to the direction of the force it opposes. To further sympathize this, let us consider some other gratis-body diagram of an object suspended by two ropes, as shown below:

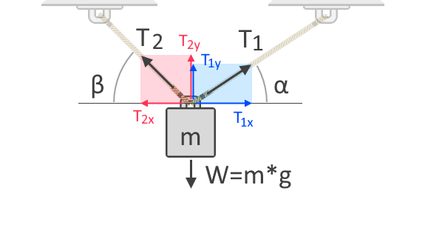
Free-body diagram of an object being suspended by two ropes showing the tension forces, their angles from the horizontal, and the forces' x and y components

In the gratuitous-body diagram shown above, we can see the horizontal and vertical components of the tension forces, T₁, and T₂. Forces are vectors, which means they always have both magnitudes and directions. Like all vectors, forces can be expressed in these components which gives the force'south influence along the horizontal and vertical axes. T₁ₓ and T₂ₓ are the vertical components of T₁ and T₂, respectively. On the other hand, T₁ᵧ and T₂ᵧ are the vertical components of the same forces, respectively. Since gravity acts on the object in the vertical axis, we demand to consider the tension forces' vertical components for our summation of forces as follows:

ΣF↑ = 0 = T₁ᵧ + T₂ᵧ + (-W)

W = T₁ᵧ + T₂ᵧ

Considering nosotros as well know the angles of the tension forces, we can limited T₁ᵧ and T₂ᵧ in terms of T₁ and T₂, respectively, with the aid of trigonometric functions:

T₁ᵧ = T₁ * sin(α)

T₂ᵧ = T₂ * sin(β)

W = T₁ * sin(α) + T₂ * sin(β)

We can also say that for the organisation to be in equilibrium, the object should non movement horizontally or along the x-axis. Therefore, the horizontal components of T₁ and T₂ must then equate to zero. Also, with the help of trigonometry, we can limited T₁ₓ and T₂ₓ in terms of T₁ and T₂, respectively:

T₁ₓ = T₂ₓ

T₁ * cos(α) = T₂ * cos(β)

If we divide both sides past cos(α), we obtain an equation wherein T₁ is expressed in terms of T₂ and the angles:

T₁ = T₂ * cos(β) / cos(α)

We tin then use this equation to solve for T₂ past substituting T₂ * cos(β) / cos(α) every bit the T₁ in our summation of forces equation, every bit shown below:

W = T₁ * sin(α) + T₂ * sin(β)

W = T₂ * [cos(β) / cos(α)] * sin(α) + T₂ * sin(β)

W = T₂ * [cos(β) * sin(α) / cos(α) + sin(β)]

T₂ = Due west / [cos(β) * sin(α) / cos(α) + sin(β)]

Finally, if we multiply this entire equation by cos(β) / cos(α) equally nosotros derived in the value of T₁ in terms of T₂, and and so simplifying everything, we go this equation:

T₁ = W / [cos(β) * sin(α) / cos(α) + sin(β)] * [cos(β) / cos(α)]

T₁ = Due west / [cos(α) * sin(β) / cos(β) + sin(α)]

At present all you lot need to know are the angles of the tension ropes with respect to the horizontal. If an angle from the vertical is given, just subtract this angle from 90°. Doing so will provide you with the angle from the horizontal. Yet, if y'all are given other values of angles that may be greater than 90° or even 180°, you might want to check out our reference bending calculator to help yous make up one's mind the angle y'all demand. Afterward determining the values for the variables in our tension force formulas, we can now solve for the tension forces.